In this article, we will learn about tuning a Simple Multilayer Perceptron model using advanced Hyperparameters tuning techniques.
In our previous articles we have learned to construct basic Multi-layered Perceptron models for both Classification and Regression problems.
Artificial Neural Network Explained with an Regression Example
Deep Learning – Classification Example
Those are very simple construction of a model and explained with details.
Basic MLP:
We know that MLP is a simple/basic neural network for simple regression/classification tasks and which can achieved using Keras.
Lets take one more step and work with simple images.
MNIST Dataset:
The MNIST database is a collection of handwritten digits. It is one of the best dataset for new Neural Network learners and people who want to try different techniques in processing images.
This dataset has a training set of 60,000 examples, and a test set of 10,000 examples. It is a subset of a larger set available from NIST. The digits have been size-normalized and centered in a fixed-size image.
The official page of MNIST dataset is http://yann.lecun.com/exdb/mnist/.
Download the below files (Originally available in MNIST website):
train-images-idx3-ubyte.gz: training set images (9912422 bytes)
train-labels-idx1-ubyte.gz: training set labels (28881 bytes)
t10k-images-idx3-ubyte.gz: test set images (1648877 bytes)
t10k-labels-idx1-ubyte.gz: test set labels (4542 bytes)
Also this dataset is available in Keras library itself:
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from keras.datasets import mnist
from keras.models import Sequential
from keras.utils.np_utils import to_categorical
Using TensorFlow backend.
Load Dataset:
(X_train, y_train), (X_test, y_test) = mnist.load_data()
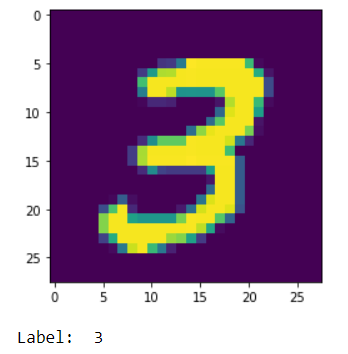
# show a number from the dataset
plt.imshow(X_train[7])
plt.show()
print('Label: ', y_train[7])
The numpy arrays X_train & X_test contains the images and y_train & y_test contains the labels.
Y value will be any number from 0 to 9.
X_train.shape, y_train.shape, X_test.shape, y_test.shape
((60000, 28, 28), (60000,), (10000, 28, 28), (10000,))
Here, notice that the image arrays X_train & X_test are in 3D array and labels are in 1D array.
Lets see the shape of a single image.
X_train[0].shape
(28, 28)
These handwritten digits images will originally look as shown below:
Okay, Lets get back to the model now.
Pre-Process X data:
We are going to make a model with Keras Sequential() Dense input layer.
As we know a black & white image is 2 Dimensional. A color image will have another dimension Channel. So it is 3D.
The Dense layer will only be applied on last axis of the image. For example, the image is of 2D say (dim_1, dim_2) then the Dense layer will be applied only on deim_2.
If the image is of 3D say (dim_1, dim_2, dim_3), then the dense layer will be applied only on dim_3.
So if we send the image as it is to the Dense layer, the last axis dim_2/dim_3 only be taken in account and the features will be considered in the model (i.e. weights will be assigned only in last axis).
To make the Dense layer to work on entire image without missing any features, we just flatten the image (numpy array) to single dimensional.
# To Flatten the image, reshaping X data: (n, 28, 28) => (n, 784)
# n => number of images. The actual size of a single image is (28, 28)
X_train = X_train.reshape((X_train.shape[0], -1))
X_test = X_test.reshape((X_test.shape[0], -1))
In this experiment, we only use the 33% of data to avoid complexity of execution.
X_train, _ , y_train, _ = train_test_split(X_train, y_train, test_size = 0.67, random_state = 7)
Pre-Process Y data:
If the output is a binary classification, then the number of nodes in output layer is one.
If the output is a multi-class classification, then the number of nodes in output layer should be the number of classes.
In our example, the label data is a number. But the output layer needs to fire any one value from 0 to 9. So we have to construct an output layer of 10 nodes.
If the model predicts the image as number “2”, then the output layer should fire the node which is allocated for “2”. i.e. it will result “1”. All other nodes should be 0. So, the output array will be [0 0 1 0 0 0 0 0 0 0].
To change the label values to an array of 10 binary values, we can use the one-hot encoding on the target value.
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
(19800, 784) (10000, 784) (19800, 10) (10000, 10)
Basic MLP model using Keras:
Naïve MLP model:
from keras.models import Sequential
from keras.layers import Activation, Dense
from keras import optimizers
model = Sequential()
model.add(Dense(50, input_shape = (784, )))
model.add(Activation('sigmoid'))
model.add(Dense(50))
model.add(Activation('sigmoid'))
model.add(Dense(50))
model.add(Activation('sigmoid'))
model.add(Dense(50))
model.add(Activation('sigmoid'))
model.add(Dense(10))
model.add(Activation('softmax'))
We use the stochastic gradient descent optimizer here and compile the model with loss function “categorical_crossentropy” as it is a classification model.
sgd = optimizers.SGD(lr = 0.001)
model.compile(optimizer = sgd, loss = 'categorical_crossentropy', metrics = ['accuracy'])
Fit the model with the batch size of 256.
validation_split = 0.3: internally split 30% of data as a validation dataset and validate the model while training itself.
verbose is 0: Less log while fitting the model.
history = model.fit(X_train, y_train, batch_size = 256, validation_split = 0.3, epochs = 100, verbose = 0)
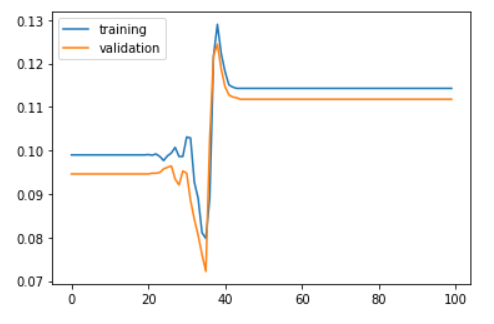
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.legend(['training', 'validation'], loc = 'upper left')
plt.show()
results = model.evaluate(X_test, y_test)
7872/10000 [======================>.......] - ETA: 0s
print('Test accuracy: ', results[1])
Test accuracy: 0.1135
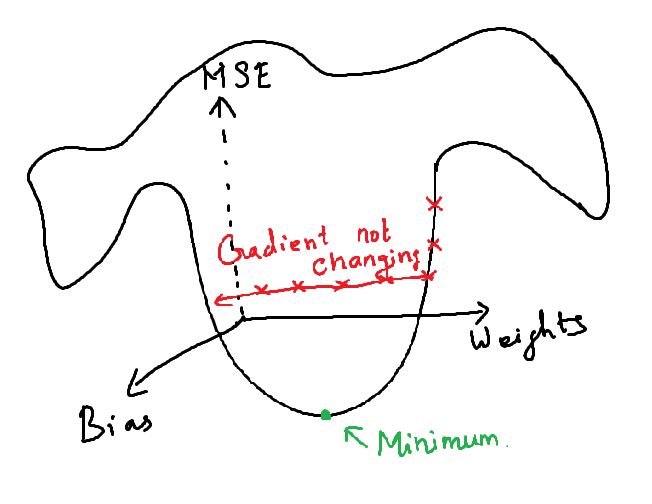
What is a Vanishing Gradient Problem?
In the above model, the test accuracy is very low. This is because the accuracy did not change after around 45th epoch. After this, the model provides same accuracy. i.e. The model did not learn anything after the 45th epoch.
The loss value was not reduced after the 45th iteration. This happens as the gradient value doesn’t change after certain iterations and this will no longer converge to the optimum value as there is no change in the gradient.
i.e., At each epoch, the weights will be adjusted in the back propagation. At each epoch, the gradients become smaller and reaches 0. Once, the gradients become 0, there will be no change in the weights. The weights remain same in all the remaining epochs. When this 0 Gradient happens in middle of the network (i.e., deep inside the network), the gradient descent will never converges to the optimum.
This issue is called vanishing gradient problem.
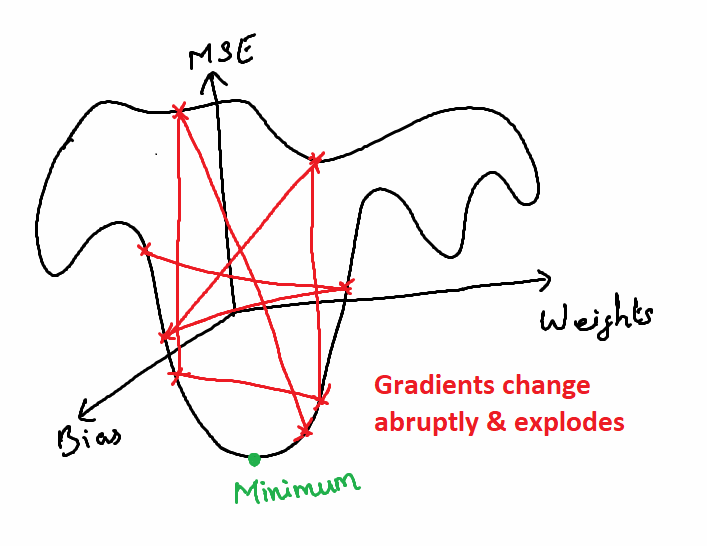
What is an Exploding Gradient Problem?
In some other cases, when all the neurons produce high positive values or when all the neurons produce very low values together, the loss value of the next iteration value will also have high variance from the previous iteration’s loss value. This will result in an unstable network and the there will be no learning.
There is a possibility of weights become NaN when the it becomes very large in further computations and so it will never converge. This problem is called Exploding Gradient problem.
Deep learning was abandoned for long time after its discovery due to this problem.
This problem has been solved after the discovery of the below techniques:
- Weight Initialization
- Nonlinearity (Activation function)
- Optimizers
- Batch Normalization
- Dropout (Regularization)
Hyperparameter Tuning Techniques:
1. Weight Initialization
In the previous experiment, the model faced vanishing gradient problem and so there was no improvement after 45th epoch.
How to resolve vanishing gradient problem?
When the weights are assigned to keras layers, a scheme will be followed.
By default, the Dense layer will use “glorot_uniform” as default kernel initializer when no initializers are mentioned explicitly in dense layer. Dense layer documentation: https://keras.io/api/layers/core_layers/dense/
The weights are an important parameter of the model, which will be optimized to get a global minimum for better accuracy.
By adjusting the weight initialization scheme, the model can be improved and vanishing gradient problem can be prevented up to some degree.
In the paper written by researchers Xavier Glorot, Antoine Bordes, and Yoshua Bengio, they proposed an initialization strategy with uniform distribution.
With the help of Normalization, the weights should be chosen such that “the mean of all weights is 0” with the standard deviation based on number of inputs and outputs.
This initialization’s implementation is provided in Keras in the name “he_normal” and it is called Xavier & He Initialization.
Keras also provides various types of initializers. We can find all of them here.
Using He_Normal Initializer:
# Create a function to generate and return models.
def mlp_model():
model = Sequential()
model.add(Dense(50, input_shape = (784, ), kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('sigmoid'))
model.add(Dense(50, kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('sigmoid'))
model.add(Dense(50, kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('sigmoid'))
model.add(Dense(50, kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('sigmoid'))
model.add(Dense(10, kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('softmax'))
sgd = optimizers.SGD(lr = 0.001)
model.compile(optimizer = sgd, loss = 'categorical_crossentropy', metrics = ['accuracy'])
return model
model = mlp_model()
history = model.fit(X_train, y_train, validation_split = 0.3, epochs = 100, verbose = 0)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.legend(['training', 'validation'], loc = 'upper left')
plt.show()
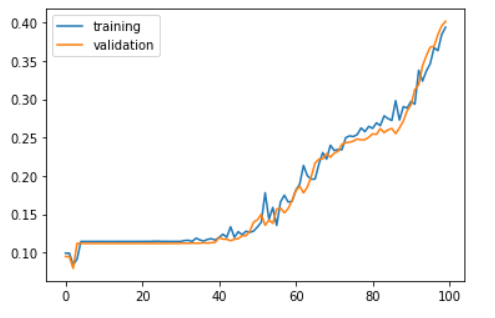
Now we can see that the accuracy is keep changing till 100th epoch even though the final accuracy is very less. However the model learns till the end.
results = model.evaluate(X_test, y_test)
9056/10000 [==========================>...] - ETA: 0s
print('Test accuracy: ', results[1])
Test accuracy: 0.4219
This solution is not enough.
2. Activation function: (Nonlinearity)
Sigmoid functions has less saturation and the values will be ranged between 0 to +1. This will cause make training slower.
When the inputs to activation function is very large or very low, it will be changed to 1 or 0 respectively.
When the gradients are small, there is a high possibility to become 0 which is the vanishing gradient problem.
The best alternative of Sigmoid Function are ReLU, ELU, Leaky ReLU and Tanh.
These activation functions provide more saturation region than Sigmoid. However ReLU, ELU & Leaky ReLU provide higher saturation regions. These can mitigate Vanishing & Exploding Gradients problem.
For more information: https://devskrol.com/2020/11/08/how-neurons-work-and-how-artificial-neuron-mimics-neurons-in-human-brain/
Using ReLU &
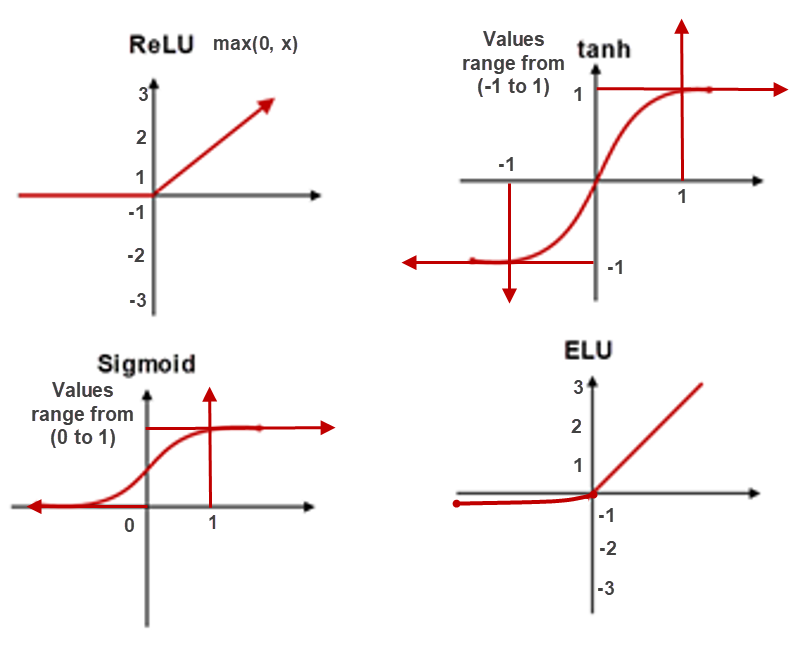
In the below program, the ReLU function solves the vanishing gradient problem.
def mlp_model():
model = Sequential()
model.add(Dense(50, input_shape = (784, )))
model.add(Activation('relu')) # use relu
model.add(Dense(50))
model.add(Activation('relu')) # use relu
model.add(Dense(50))
model.add(Activation('relu')) # use relu
model.add(Dense(50))
model.add(Activation('relu')) # use relu
model.add(Dense(10))
model.add(Activation('softmax'))
sgd = optimizers.SGD(lr = 0.001)
model.compile(optimizer = sgd, loss = 'categorical_crossentropy', metrics = ['accuracy'])
return model
model = mlp_model()
history = model.fit(X_train, y_train, validation_split = 0.3, epochs = 100, verbose = 0)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.legend(['training', 'validation'], loc = 'upper left')
plt.show()
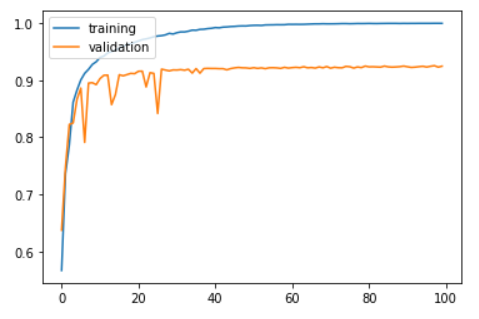
Now, training and validation accuracy improve instantaneously, but reach a plateau after around 30 epochs.
results = model.evaluate(X_test, y_test)
8512/10000 [========================>.....] - ETA: 0s
print('Test accuracy: ', results[1])
Test accuracy: 0.9188
3. Optimizers
Optimizers are algorithms used to adjust the parameters (weights and learning rates) to reduce the loss/errors.
When discussing about Optimization and Optimizers, the first word comes to our mind is Gradient Descent. There are some major variations of Gradient Descents.
Batch Gradient Descent: Take the entire data set and computes the Gradient Descent.
i.e. For each epochs, the entire dataset is used in the calculation of MSE.
Stochastic Gradient Descent: Takes 1 random sample from the entire dataset.
Many variants of SGD are proposed and used nowadays. However all the optimizers has their own shortcomings. We can choose the optimizer based on the issue and usage.
One of the most popular ones are Adam (Adaptive Moment Estimation)
The below animation is an excellent illustration of comparison of optimizers made by Alec Radford. Unfortunately the Adam optimizer is not mentioned in this illustration.
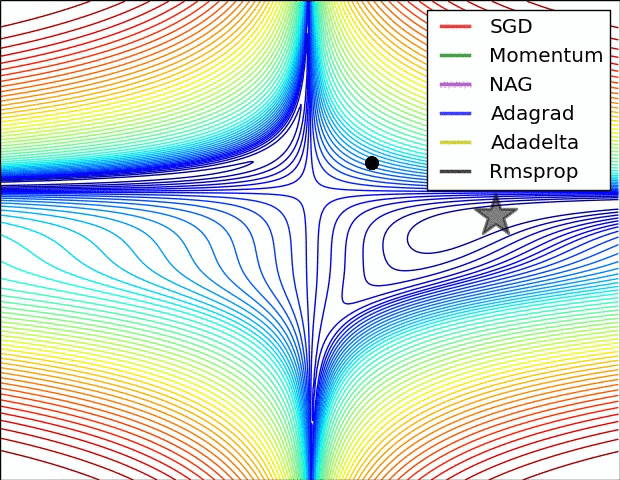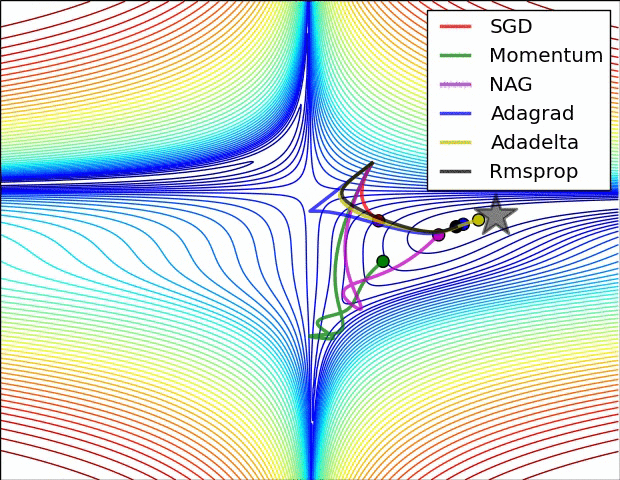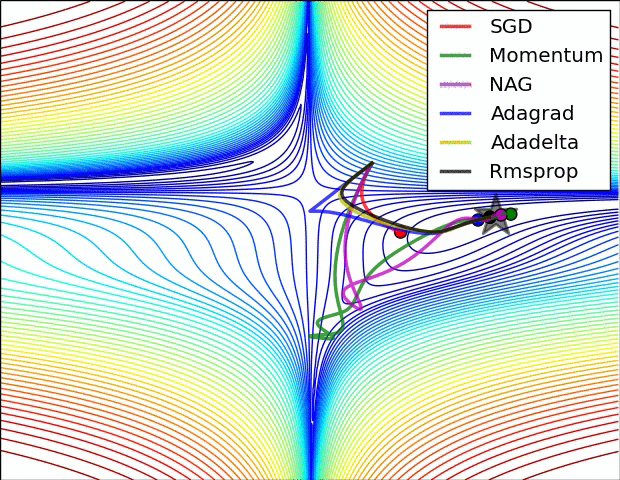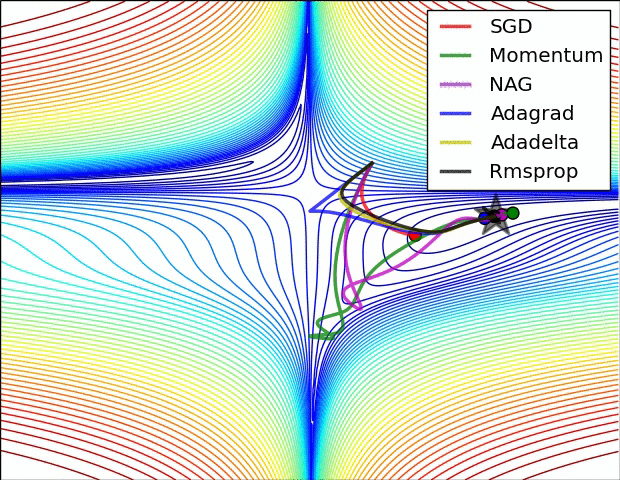
Using Adam optimizer:
def mlp_model():
model = Sequential()
model.add(Dense(50, input_shape = (784, )))
model.add(Activation('elu'))
model.add(Dense(50))
model.add(Activation('elu'))
model.add(Dense(50))
model.add(Activation('elu'))
model.add(Dense(50))
model.add(Activation('elu'))
model.add(Dense(10))
model.add(Activation('softmax'))
adam = optimizers.Adam(lr = 0.001) # use Adam optimizer
model.compile(optimizer = adam, loss = 'categorical_crossentropy', metrics = ['accuracy'])
return model
model = mlp_model()
history = model.fit(X_train, y_train, validation_split = 0.3, epochs = 100, verbose = 0)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.legend(['training', 'validation'], loc = 'upper left')
plt.show()
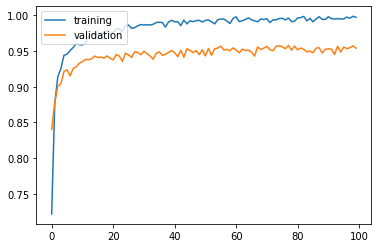
Training and validation accuracy improve instantaneously, but reach plateau after around 50 epochs.
results = model.evaluate(X_test, y_test)
9792/10000 [============================>.] - ETA: 0s
print('Test accuracy: ', results[1])
Test accuracy: 0.9516
4. Batch Normalization
Another technique that was proposed to solve the vanishing gradient problem is batch Normalization.
Batch Normalization takes place immediate before the activation function of the layer. All the inputs of the current batch’s activation layer will be zero-centered and then passed to Activation functions.
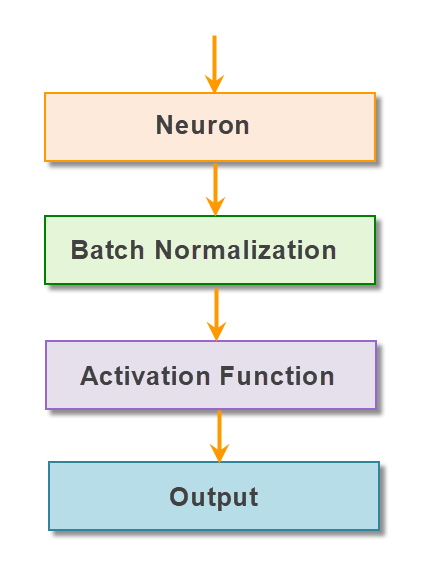
Batch normalization layer is usually inserted after dense/convolution and before nonlinearity:
from keras.layers import BatchNormalization
def mlp_model():
model = Sequential()
model.add(Dense(50, input_shape = (784, )))
model.add(BatchNormalization()) # Add Batchnorm layer before Activation
model.add(Activation('elu'))
model.add(Dense(50))
model.add(BatchNormalization()) # Add Batchnorm layer before Activation
model.add(Activation('elu'))
model.add(Dense(50))
model.add(BatchNormalization()) # Add Batchnorm layer before Activation
model.add(Activation('elu'))
model.add(Dense(50))
model.add(BatchNormalization()) # Add Batchnorm layer before Activation
model.add(Activation('elu'))
model.add(Dense(10))
model.add(Activation('softmax'))
adam = optimizers.Adam(lr = 0.001)
model.compile(optimizer = adam, loss = 'categorical_crossentropy', metrics = ['accuracy'])
return model
model = mlp_model()
history = model.fit(X_train, y_train, validation_split = 0.3, epochs = 100, verbose = 0)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.legend(['training', 'validation'], loc = 'upper left')
plt.show()
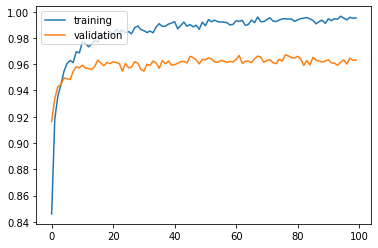
Training and validation accuracy improve consistently, but reach plateau after around 60 epochs:
results = model.evaluate(X_test, y_test)
9920/10000 [============================>.] - ETA: 0s
print('Test accuracy: ', results[1])
Test accuracy: 0.9643
5. Dropout (Regularization)
When the networks grow deeper, there is a chance of too much of learning the training data and overfit to it.
In the previous results, you can notice that the validation accuracy and training accuracies differ from each other. This is a sign of overfitting.
Dropout is a simple and powerful way to prevent overfitting. Some neurons will be randomly selected and dropped from the network in each layer.
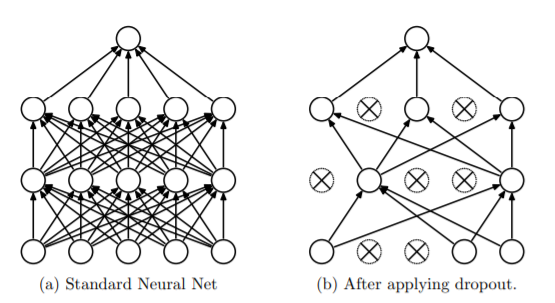
Right: After applying dropout to the network on the left.
Source: Journal on Dropout
from keras.layers import Dropout
def mlp_model():
model = Sequential()
model.add(Dense(50, input_shape = (784, )))
model.add(Activation('elu'))
model.add(Dropout(0.2)) # Dropout layer after Activation
model.add(Dense(50))
model.add(Activation('elu'))
model.add(Dropout(0.2)) # Dropout layer after Activation
model.add(Dense(50))
model.add(Activation('elu'))
model.add(Dropout(0.2)) # Dropout layer after Activation
model.add(Dense(50))
model.add(Activation('elu'))
model.add(Dropout(0.2)) # Dropout layer after Activation
model.add(Dense(10))
model.add(Activation('softmax'))
adam = optimizers.Adam(lr = 0.001)
model.compile(optimizer = adam, loss = 'categorical_crossentropy', metrics = ['accuracy'])
return model
model = mlp_model()
history = model.fit(X_train, y_train, validation_split = 0.3, epochs = 100, verbose = 1)
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.legend(['training', 'validation'], loc = 'upper left')
plt.show()
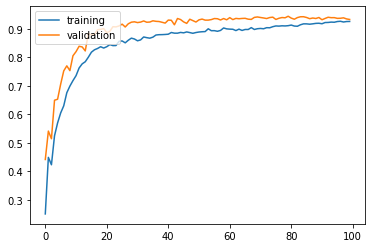
The validation and training results seems to be similar. Hence, applying dropout is one of the simple way to mitigate overfitting.
results = model.evaluate(X_test, y_test)
8640/10000 [========================>.....] - ETA: 0s
print('Test accuracy: ', results[1])
Test accuracy: 0.9309
Hyperparameter tuning cannot be done with a set of fixed steps. These are the ways of tuning the algorithm’s parameters to get the best from the algorithm.
So we can further make changes in the parameters, number of layers, number of nodes in each layer to get the best result.