Decision Trees

In this article we will learn about what is Decision Tree and How it works. How it gets Overfitted and how can we resolve Overfitting.

What are Decision Trees?

Decision Tree is a rule-based algorithm in which, to predict a result we answer a set of questions and come up to a decision.

If we illustrate this process in a diagram that can be easily understandable to everyone, it comes up like a tree.

In real life we might have come across a situation in which we have a questionnaire session and finally we get a solution.

For example: To check whether a patient is ready for “CT scan with Contrast”. Ready if 1. Patient is allowed to drink clear liquid but not solid food, three hours prior to their CT scan examination.

• Did you Eat? Or Drink?
  • If Eat – Rejected
  • If Drink – Did you consume only clear liquids?
    • If Yes – Eligible for Examination,
    • If No – Rejected.

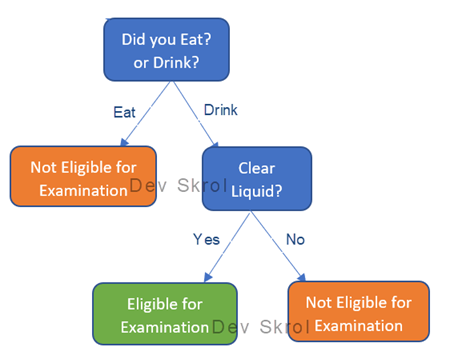
Now, we can clearly understand that how useful a questionnaire is.

We are going to steal this technique to predict target variable and we call it as Decision Tree.

Isn’t this technique reminding you about Flow Chart and easy to understand?

In the above tree, each box identified as a Node.

The first Node is called the Root Node.

The Nodes in Orange and Green are final result of the Questionnaire. These Nodes are called Terminal Nodes, which has the final Answer.

All the remaining intermediate Nodes are called Internal Nodes.

How the Decision Tree Algorithm Works:

As the questioning person knows on what factor should be considered first and what decision should be taken, it’s easy for them to decide. This is how humans can think.

But how the machine can work on it?

How can a program can identify which question comes first?

In our previous “CT scan with Contrast” example, we need to find which question out of all possible questions make a short questionnaire to come up with a decision.

We segregated the Eat and Drunk people in the first step itself. So, we can reject who consumed solid food in first step itself. Think of the other way and come up with your steps. You will see 1 or few more steps finally.

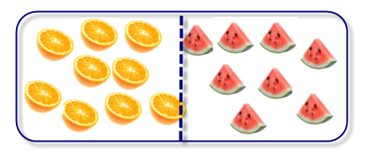
In the below Image #1, if you want to separate oranges and watermelons by a horizontal or vertical line, then the best line that separates well would be a vertical line in the middle. Agree?

If it is a Vertical Line, then the feature existing in X axis plays here.

i.e. We want to make both divided parts should have similar class values. In that way we can decide that whatever comes the left category should be an orange and whatever comes right should be a watermelon.

For example, in the below Image #3, you can see that the first three pictures are not partitioning well to segregate the items. In the 4^th picture, it is the most possible good partitioning, so that the further steps for partitioning is minimized.

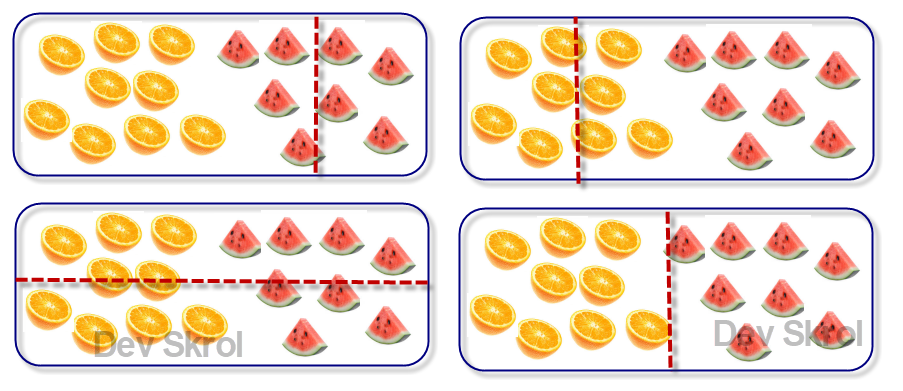
Now after dividing the data, the two regions are having same type of fruits (Same Class Values). We call it as “Purity”.

How can a Machine find this best line and find the purity of Nodes?

To do so, first we need to pick the first Root Node and where to split.

This will be done using anyone of the below 2 methods:

1. Information Gain (Uses Entropy).
2. Gini Index.

Both Gini and Entropy talks about the “The measure of Uncertainty”.

In the above Pictures, A is pure as it is having only 1 class. B has impurity but it can give medium knowledge on what class is dominating the region. But in C it has equal number of Suns and Stars. We cannot come up with any decision here. This node has high impurity.

Information Gain (Uses Entropy):

Information gain = Entropy of target – Entropy of attribute

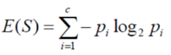
In our example, Entropy of Target is Entropy of the Fruit Column. Entropy of attribute is nothing but the entropy of a feature (predictors/ Columns).

Let’s take,

Information Gain by Shape = Entropy of Fruit – Entropy of Shape = 0.25

Information Gain by Color = Entropy of Fruit – Entropy of Color = 0.35

Here the Entropy of Colour is highest Value.

So, Color will be the Root Node.

Gini Index:

The Gini Index is calculated by subtracting the sum of the squared probabilities of each class from one.

Here Pj is the probability of an object being classified to a particular class.

Let’s take,

Gini Index by Shape = 0.31

Gini Index by Colour = 0.23

Here the Gini Index of Colour is the lowest Value.

So, Color will be the Root Node.

Gini Index Vs Information Gain:

Gini Index or Information Gain (Entropy), both works similar except that the formula is different.

Each feature will be taken and the Gini Index will be calculated. A feature that gives Lowest Gini score is used as Root Node or Decision Node.

Similarly, for each feature the entropy value is calculated and then the Information Gain score is calculated for that feature. Finally the feature that gives Highest Information Gain will be taken as Root Node or Decision Node.

Similarly, the remaining internal nodes will be split further using Gini/Entropy.

However, we can control this parameter in algorithm.

Entropy is the oldest Method that uses Log in computation. So, it is slower than Gini Score calculation.

So, Gini Index is the most used method as it is faster than Entropy. But both the methods will provide same result.

We are not going deep into this topic in this article. I will post a new article with good and easy examples later and link it here.

Even after partitioning, if there are still different type of fruits, the algorithm will again divide the region in which different types of fruit exists. This will be done using given features and come up with the terminal Node as Pure Node (A Node having single class).

A Decision tree can also work for Regression Problem to predict Continuous values.

In Classification Problem, best partition is made by checking the purity. In Regression, it is done by checking the least Variance.

Another Example:

Let’s make a model to predict what fruit it is by using the given size and colour of the fruits.

If we are given with size and colour of the fruits, then we can separate by colour first.

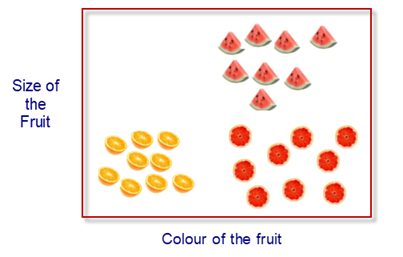
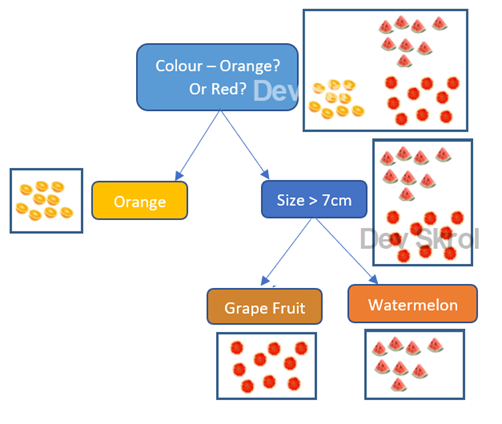
In the above “Decision Tree” you can see that, first the color is taken to divide regions, the results are Orange and Red.

In which Orange is a pure Node, where there is only a single class exists.

But Red has impurity as there are two types of fruits with in that region (Two classes exist in that region).

when using size, we can divide by, size > a particular centimetre. Should it be 7cm? or 5cm? Which will make the result better?

Internally the machine tries all the possible values and check the variance of the resultant regions.

For a value of 7cm, if the purity is good then the machine will take 7cm as boundary to divide the region.

Finally, we got the Pure nodes for Grape Fruit & Watermelon.

Overfitting in Decision Tree:

In the previous example, there are no noises in data. The data itself is clean and we get the pure Node in one or two splits.

What if there are lots of Noises in data?

In the above example, The Root node is the blue line. The Root Node’s condition is X1> 4.3

The yellow line is the second level. X2 > 3.5

Now the region R3 is Pure. This m=could be a terminal Node.

But the R1 and R2 Regions are still having impurity.

The machine will then work on R1 and derive R4 region using condition “X1>3 and X1<3.5 and X2<2.5”. Possible right?

In the same way the R2 will be then purified by deriving R5.

Now all the terminal Nodes R1, R2, R3, R4 & R5 are pure.

The algorithm ends here.

But do you think this is good? The data in R4 and R5 could be a noise.

Yes! This model is Overfitting for the training data.

If the test data has a Red star fall in R4, then it will end up as error. Same happens in R5 region too.

Then how can we tell the model to stop dividing the regions at some point?

Pruning the Tree:

This is where we prune the tree by setting the parameters of the Decision Tree.

Max_depth: This parameter helps to set the maximum depth of the tree. If we set the max_depth of the above example as 3 then R4 and R5 regions will not be created.

Min_sample_split: This parameter set the minimum number of samples (rows) that is required for further splitting. For example, if a node is having 4 stars and 1 sun, and if we set the min_sample_split as 6, then this node cannot be divided further as this has only 5 samples.

Min_samples_leaf: This parameter can be used to mention the minimum number of samples that should present in terminal node (leaf node).

When to use Decision Tree?

We already have Logistic Algorithm for Classification and Linear for Regression. Then why we need Decision Trees? Below are the reasons and situations when you should use Decision Trees.

• If the data is Linear then we can use Logistic Regression itself. But how can we know the data is Linear or not when the Dimensions are higher?
• We can start using some basic classification techniques such as Logistic Regression. The thumb-rule is to use the simple methods. If the results are not good, then the problem may not be solved by linear classification methods and we may need to use more complex non-linear classifier algorithms.
• If Logistic and DT are giving same results then why we need to go for a complex time-consuming algorithm.
• If data is unbalanced, then the best choice is Decision Tree.
• If the number of features is high (example > 100) and sample is less (data = 100000), then we can use Logistic Regression as Decision Tree is slow when number of features is high.
• If the number of features is higher than the number of samples, then we should not use Logistic Regression.
• Decision trees are prone to Overfitting.
• The one of the best things with Decision Tree is this algorithm does not require Scaling.
• As we can see how the decision tree split the data, Decision Tree is a White Box algorithm.

Conclusion:

In this article we learned about Decision Tree.

We also found overfitting issue in Decision Trees. There is a way to fix it! Please check this article: Overcomes Overfitting problem of Decision Trees – Check advantages Section.

I will add a new post to practice Decision Tree in Python.

Happy Programming! 🙂

Like to support? Just click the heart icon ❤️.